from config import *
from config import make_df_ECB
%matplotlib inlineLa curva di Phillips
Introduzione
Nel finire degli anni 50 l’economista della LSE A.W.Phillips osservò una relazione inversa fra disoccupazione e inflazione salariale, ovvero il tasso di crescita dei salari nominali, nell’economia britannica. Pochi anni dopo, Samuelson e Solow mostrarono che una simile relazione esisteva anche nell’economia americana, legando non più la disoccupazione solamente all’inflazione salariale, ma al tasso di crescita generale dei prezzi. La curva divenne così uno strumento utilizzato dai policy makers che, dopo aver valutato il trade-off tra inflazione e disoccupazione, mettevano in atto strategie atte a raggiungere un punto specifico della curva.
Paper di Phillips
In questa sezione, replicheremo l’articolo originale di Phillips, utilizzando i dati forniti dalla Bank Of England (https://www.bankofengland.co.uk/statistics/research-datasets)
# Importa i dati sulla disoccupazione dal file Excel contenente dati macroeconomici del Regno Unito
unemployment = pd.read_excel('a-millennium-of-macroeconomic-data-for-the-uk.xlsx',
sheet_name='A50. Employment & unemployment',
skiprows=2, usecols='A,J')
# Rimuove le prime due righe che contengono informazioni non necessarie
unemployment = unemployment[2:]
# Rinomina la colonna non etichettata in 'Year' per maggiore chiarezza
unemployment.rename(columns={'Unnamed: 0': 'Year'}, inplace=True)
# Imposta l'anno come indice del DataFrame
unemployment.set_index('Year', inplace=True)
# Converte la colonna del tasso di disoccupazione in formato numerico (float)
unemployment['Unemployment rate'] = unemployment['Unemployment rate'].astype(float)
# Mostra le prime righe del DataFrame per verificare la corretta importazione dei dati
unemployment.head()| Unemployment rate | |
|---|---|
| Year | |
| 1855 | 3.731877 |
| 1856 | 3.518180 |
| 1857 | 3.945176 |
| 1858 | 5.215345 |
| 1859 | 3.276380 |
# Importa i dati sui salari e l'inflazione dal file Excel contenente dati macroeconomici del Regno Unito
wages_inflation = pd.read_excel('a-millennium-of-macroeconomic-data-for-the-uk.xlsx',
sheet_name='A47. Wages and prices',
usecols='A,BD')
# Rinomina le colonne per una maggiore chiarezza
wages_inflation.columns = ['Year', 'Wage index']
# Rimuove le prime sei righe non necessarie
wages_inflation = wages_inflation[6:]
# Converte la colonna 'Year' in formato intero
wages_inflation['Year'] = wages_inflation['Year'].astype(int)
# Converte la colonna 'Wage index' in formato numerico (float)
wages_inflation['Wage index'] = wages_inflation['Wage index'].astype(float)
# Filtra i dati per includere solo gli anni a partire dal 1855
wages_inflation = wages_inflation[wages_inflation['Year'] >= 1855]
# Imposta l'anno come indice del DataFrame
wages_inflation.set_index('Year', inplace=True)
# Calcola la differenza centrale prima (approssimazione numerica della derivata prima) e la esprime in percentuale.
# Questa è la misura utilizzata nell'articolo originale, qui utilizzeremo invece la variazione percentuale
wages_inflation['First central difference'] = (
(wages_inflation['Wage index'].shift(-1) - wages_inflation['Wage index'].shift(1)) /
(2 * wages_inflation['Wage index'])
) * 100
# Calcola la variazione percentuale anno su anno del Wage index
wages_inflation['Percent change'] = wages_inflation['Wage index'].pct_change() * 100
# Mostra le prime righe del DataFrame per verificare la corretta elaborazione dei dati
wages_inflation.head()| Wage index | First central difference | Percent change | |
|---|---|---|---|
| Year | |||
| 1855 | 59.0 | NaN | NaN |
| 1856 | 59.0 | -1.694915 | 0.000000 |
| 1857 | 57.0 | -2.631579 | -3.389831 |
| 1858 | 56.0 | 0.000000 | -1.754386 |
| 1859 | 57.0 | 1.754386 | 1.785714 |
# Unisce i DataFrame 'unemployment' e 'wages_inflation' utilizzando l'indice (Year) e rimuove eventuali valori NaN
df = pd.merge(unemployment, wages_inflation, right_index=True, left_index=True).dropna()
# Suddivide il dataset in tre periodi storici distinti per analizzare la relazione tra disoccupazione e inflazione salariale
dfA = df[df.index <= 1913].copy() # Periodo pre-1913
dfB = df[(df.index >= 1913) & (df.index <= 1948)].copy() # 1913-1948 (tra le due guerre)
dfC = df[(df.index >= 1948) & (df.index <= 1957)].copy() # 1948-1957 (primi anni post-bellici)
# Definisce le etichette temporali per i grafici
dates = ['1861-1913', '1913-1948', '1948-1957']
# Crea una figura con tre subplot affiancati per rappresentare ciascun periodo
fig, ax = plt.subplots(1, 3, figsize=(10, 3.5))
# Itera sui tre sotto-dataset per stimare e tracciare la curva di Phillips per ciascun periodo
for i, _ in enumerate([dfA, dfB, dfC]):
# Calcola il termine di aggiustamento per evitare problemi con il logaritmo
a = abs(_["Percent change"].min()) + 0.9
# Trasforma in logaritmo il tasso di inflazione salariale e il tasso di disoccupazione
_["Log wage inflation rate"] = np.log(_["Percent change"] + a)
_["Log unemployment rate"] = np.log(_["Unemployment rate"])
# Definisce le variabili per la regressione lineare (modello di Phillips)
X = _["Log unemployment rate"]
Y = _["Log wage inflation rate"]
X = sm.add_constant(X) # Aggiunge l'intercetta al modello di regressione
model = sm.OLS(Y, X).fit() # Stima il modello di regressione
R2 = model.rsquared # Ottiene il coefficiente di determinazione R^2
# Calcola i valori predetti dalla regressione e li riconverte dalla scala logaritmica
_["Predicted log wage inflation rate"] = model.predict(X)
_["Predicted wage inflation rate"] = np.exp(_["Predicted log wage inflation rate"]) - a
# Ordina i dati per il tasso di disoccupazione per una migliore rappresentazione grafica
sorted_data = _.sort_values(by='Unemployment rate')
# Disegna una linea orizzontale per rappresentare l'asse y=0
ax[i].axhline(y=0, color='silver', linewidth=2)
# Crea uno scatter plot con i dati osservati
ax[i].scatter(_['Unemployment rate'], _['Percent change'], alpha=0.7,
label="Osservazioni", color=bmh_colors[0])
# Disegna la curva di Phillips stimata dalla regressione
ax[i].plot(sorted_data['Unemployment rate'], sorted_data['Predicted wage inflation rate'],
color=bmh_colors[1], label="Curva Di Phillips")
# Imposta il titolo per ciascun sottografico
ax[i].set_title(f"UK, {dates[i]}", loc='left')
# Etichette degli assi
ax[i].set_xlabel('Tasso Di Disoccupazione')
ax[i].set_ylabel('Tasso Di Inflazione Salariale')
# Attiva la griglia
ax[i].grid(True)
# Aggiunge la legenda
ax[i].legend()
# Migliora la disposizione dei grafici per evitare sovrapposizioni
plt.tight_layout()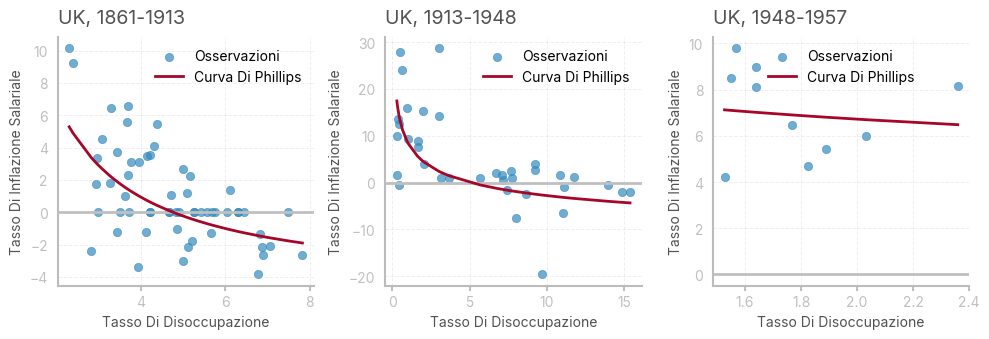
Paper di Samuelson e Solow
In questa sezione, cercheremo di analizzare il fenomeno all’interno dell’economia Americana, per la quale i dati sono purtroppo frammentari (si vedano https://data.bls.gov/pdq/SurveyOutputServlet e https://fred.stlouisfed.org/series/M08142USM055NNBR)
# Carica i dati sulla disoccupazione (BLS) dal file Excel, saltando le prime 16 righe e impostando 'Year' come indice
unemp = pd.read_excel('BLS1.xlsx', skiprows=16).set_index('Year')
# Carica i dati sulle retribuzioni orarie medie da 25 industrie manifatturiere degli Stati Uniti (NBER)
earnings = pd.read_csv('Average Hourly Earnings, Twenty-Five Manufacturing Industries for United States.csv').set_index('observation_date')
# Converte l'indice di 'earnings' in formato datetime (anno-mese-giorno)
earnings.index = pd.to_datetime(earnings.index, format='%Y-%m-%d')
# Raggruppa i dati sulle retribuzioni annualmente, calcolando la media per ogni anno
earnings = earnings.groupby(pd.Grouper(freq='Y')).mean()
# Estrae solo l'anno dall'indice per facilitarne l'elaborazione
earnings.index = earnings.index.year
# Filtra i dati per gli anni dal 1929 al 1947
earnings = earnings[(earnings.index >= 1929) & (earnings.index <= 1947)]
# Rinomina la colonna per avere una denominazione chiara
earnings.columns = ['HOURLY_WAGE']
# Rinomina la colonna della disoccupazione per chiarezza
unemp.columns = ['UNEMPLOYMENT']
# Unisce i due DataFrame sui rispettivi indici (anno)
df = pd.merge(unemp, earnings, right_index=True, left_index=True)
# Calcola la variazione percentuale annuale delle retribuzioni orarie
df['PCT_CHANGE'] = df['HOURLY_WAGE'].pct_change() * 100
# Rimuove le righe con valori mancanti (NaN) creati durante il calcolo della variazione percentuale
df = df.dropna()
# Mostra le prime righe del DataFrame per verificare i dati
df.head()| UNEMPLOYMENT | HOURLY_WAGE | PCT_CHANGE | |
|---|---|---|---|
| Year | |||
| 1930 | 8.7 | 0.589000 | -0.113058 |
| 1931 | 15.9 | 0.563833 | -4.272779 |
| 1932 | 23.6 | 0.497583 | -11.749926 |
| 1933 | 24.9 | 0.490583 | -1.406800 |
| 1934 | 21.7 | 0.579750 | 18.175641 |
# Calcola il termine di aggiustamento per evitare problemi con il logaritmo
a = abs(df["PCT_CHANGE"].min()) + 0.9
# Calcola il logaritmo del tasso di variazione percentuale delle retribuzioni, aggiungendo il termine 'a'
df["LOG_VAR_PERC"] = np.log(df["PCT_CHANGE"] + a)
# Calcola il logaritmo del tasso di disoccupazione
df["LOG_UNRATE"] = np.log(df["UNEMPLOYMENT"])
# Definisce le variabili per la regressione lineare (modello di Phillips)
X = df["LOG_UNRATE"]
Y = df["LOG_VAR_PERC"]
X = sm.add_constant(X) # Aggiunge l'intercetta al modello di regressione
model = sm.OLS(Y, X).fit() # Stima il modello di regressione
R2 = model.rsquared # Ottiene il coefficiente di determinazione R^2
# Calcola i valori predetti dalla regressione e li riconverte dalla scala logaritmica
df["Predicted log inflation rate"] = model.predict(X)
df["Predicted inflation rate"] = np.exp(df["Predicted log inflation rate"]) - a
# Ordina i dati per il tasso di disoccupazione per una migliore rappresentazione grafica
sorted_data = df.sort_values(by='UNEMPLOYMENT')
# Crea una figura con un solo sottografico
fig, ax = plt.subplots(1, 1)
# Disegna una linea orizzontale per rappresentare l'asse y=0
ax.axhline(y=0, color='silver', linewidth=2)
# Crea uno scatter plot con i dati osservati
ax.scatter(df['UNEMPLOYMENT'], df['PCT_CHANGE'], alpha=0.7, label="Osservazioni", color=bmh_colors[0])
# Disegna la curva di Phillips stimata dalla regressione
ax.plot(sorted_data['UNEMPLOYMENT'], sorted_data['Predicted inflation rate'],
color=bmh_colors[1], label="Curva Di Phillips")
# Imposta il titolo del grafico
ax.set_title(f"US, 1930-1947", loc='left')
# Etichette degli assi
ax.set_xlabel('Tasso Di Disoccupazione')
ax.set_ylabel('Tasso Di Inflazione Salariale')
# Attiva la griglia
ax.grid(True)
# Aggiunge la legenda
ax.legend()
# Migliora la disposizione dei grafici per evitare sovrapposizioni
plt.tight_layout()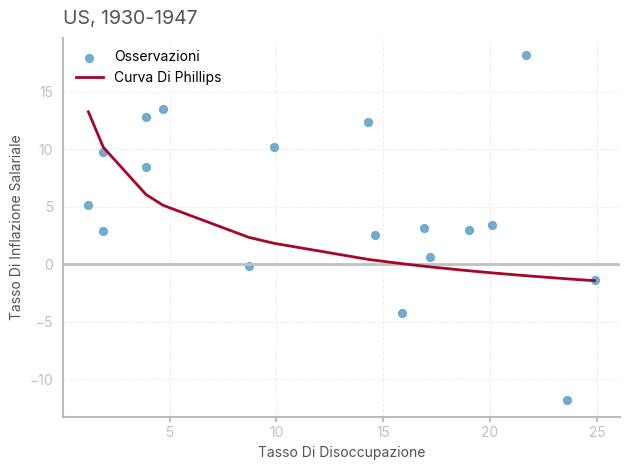
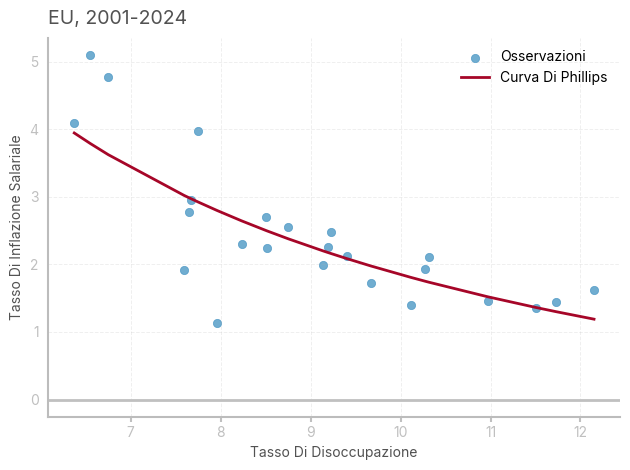
E oggi?
def make_df_ECB(key, obs_name):
"""Estrae i dati dal datawarehouse della BCE"""
url_ = 'https://sdw-wsrest.ecb.europa.eu/service/data/' # URL di base per il servizio web della BCE
format_ = '?format=csvdata' # Impostazione del formato dei dati in CSV
df = pd.read_csv(url_+key+format_) # Legge i dati CSV dal servizio web BCE usando la chiave
df = df[['TIME_PERIOD', 'OBS_VALUE']] # Seleziona le colonne di interesse (periodo e valore osservato)
df['TIME_PERIOD'] = pd.to_datetime(df['TIME_PERIOD']) # Converte il periodo in formato datetime
df = df.set_index('TIME_PERIOD') # Imposta il periodo come indice del dataframe
df.columns = [obs_name] # Rinomina la colonna con il nome della variabile
return df
# Chiave per il tasso di disoccupazione
unemp_rate_key = 'LFSI/Q.I9.S.UNEHRT.TOTAL0.15_74.T' # Codice identificativo del tasso di disoccupazione
unemp_rate = make_df_ECB(unemp_rate_key, 'Unemployment Rate') # Ottieni i dati dal database ECB
# Chiave per la wage inflation (inflazione salariale)
wage_inflation_key = 'MNA/Q.Y.I9.W2.S1.S1._Z.COM_PS._Z._T._Z.IX.V.N' # Codice identificativo del salario per addetto (indice)
wage_inflation = make_df_ECB(wage_inflation_key, 'Compensation per employee') # Ottieni i dati dal database ECB
wage_inflation = wage_inflation[wage_inflation.index >= '2000-01-01'] # Filtra i dati dal 2000 in poi
# Combina i dati di disoccupazione e salario in un unico dataframe
df = pd.merge(unemp_rate, wage_inflation, right_index=True, left_index=True)
# Raggruppa i dati per anno e calcola la media per il tasso di disoccupazione e l'ultimo valore per la compensazione per addetto
df = df.groupby(pd.Grouper(freq='Y'))[['Unemployment Rate', 'Compensation per employee']].agg({'Unemployment Rate':'mean',
'Compensation per employee':'last'})
df.index = df.index.year # Imposta l'indice come anno
df['Wage inflation rate'] = df['Compensation per employee'].pct_change()*100 # Calcola il tasso di inflazione salariale come variazione percentuale
df = df.dropna() # Rimuove i valori mancanti
df.head() # Mostra le prime righe del dataframe| Unemployment Rate | Compensation per employee | Wage inflation rate | |
|---|---|---|---|
| TIME_PERIOD | |||
| 2001 | 8.508061 | 70.332653 | 2.705440 |
| 2002 | 8.753020 | 72.127430 | 2.551840 |
| 2003 | 9.188271 | 73.757671 | 2.260224 |
| 2004 | 9.399281 | 75.327356 | 2.128164 |
| 2005 | 9.231180 | 77.193789 | 2.477762 |
# Calcola il termine di aggiustamento per evitare problemi con il logaritmo
a = abs(df["Wage inflation rate"].min()) + 0.9
# Calcola il logaritmo del tasso di variazione percentuale delle retribuzioni, aggiungendo il termine 'a'
df["LOG_VAR_PERC"] = np.log(df["Wage inflation rate"] + a)
# Calcola il logaritmo del tasso di disoccupazione
df["LOG_UNRATE"] = np.log(df["Unemployment Rate"])
# Definisce le variabili per la regressione lineare (modello di Phillips)
X = df["LOG_UNRATE"]
Y = df["LOG_VAR_PERC"]
X = sm.add_constant(X) # Aggiunge l'intercetta al modello di regressione
model = sm.OLS(Y, X).fit() # Stima il modello di regressione
R2 = model.rsquared # Ottiene il coefficiente di determinazione R^2
# Calcola i valori predetti dalla regressione e li riconverte dalla scala logaritmica
df["Predicted log inflation rate"] = model.predict(X)
df["Predicted inflation rate"] = np.exp(df["Predicted log inflation rate"]) - a
# Ordina i dati per il tasso di disoccupazione per una migliore rappresentazione grafica
sorted_data = df.sort_values(by='Unemployment Rate')
# Crea una figura con un solo sottografico
fig, ax = plt.subplots(1, 1)
# Disegna una linea orizzontale per rappresentare l'asse y=0
ax.axhline(y=0, color='silver', linewidth=2)
# Crea uno scatter plot con i dati osservati
ax.scatter(df['Unemployment Rate'], df['Wage inflation rate'], alpha=0.7, label="Osservazioni", color=bmh_colors[0])
# Disegna la curva di Phillips stimata dalla regressione
ax.plot(sorted_data['Unemployment Rate'], sorted_data['Predicted inflation rate'],
color=bmh_colors[1], label="Curva Di Phillips")
# Imposta il titolo del grafico
ax.set_title(f"EU, 2001-2024", loc='left')
# Etichette degli assi
ax.set_xlabel('Tasso Di Disoccupazione')
ax.set_ylabel('Tasso Di Inflazione Salariale')
# Attiva la griglia
ax.grid(True)
# Aggiunge la legenda
ax.legend()
# Migliora la disposizione dei grafici per evitare sovrapposizioni
plt.tight_layout()